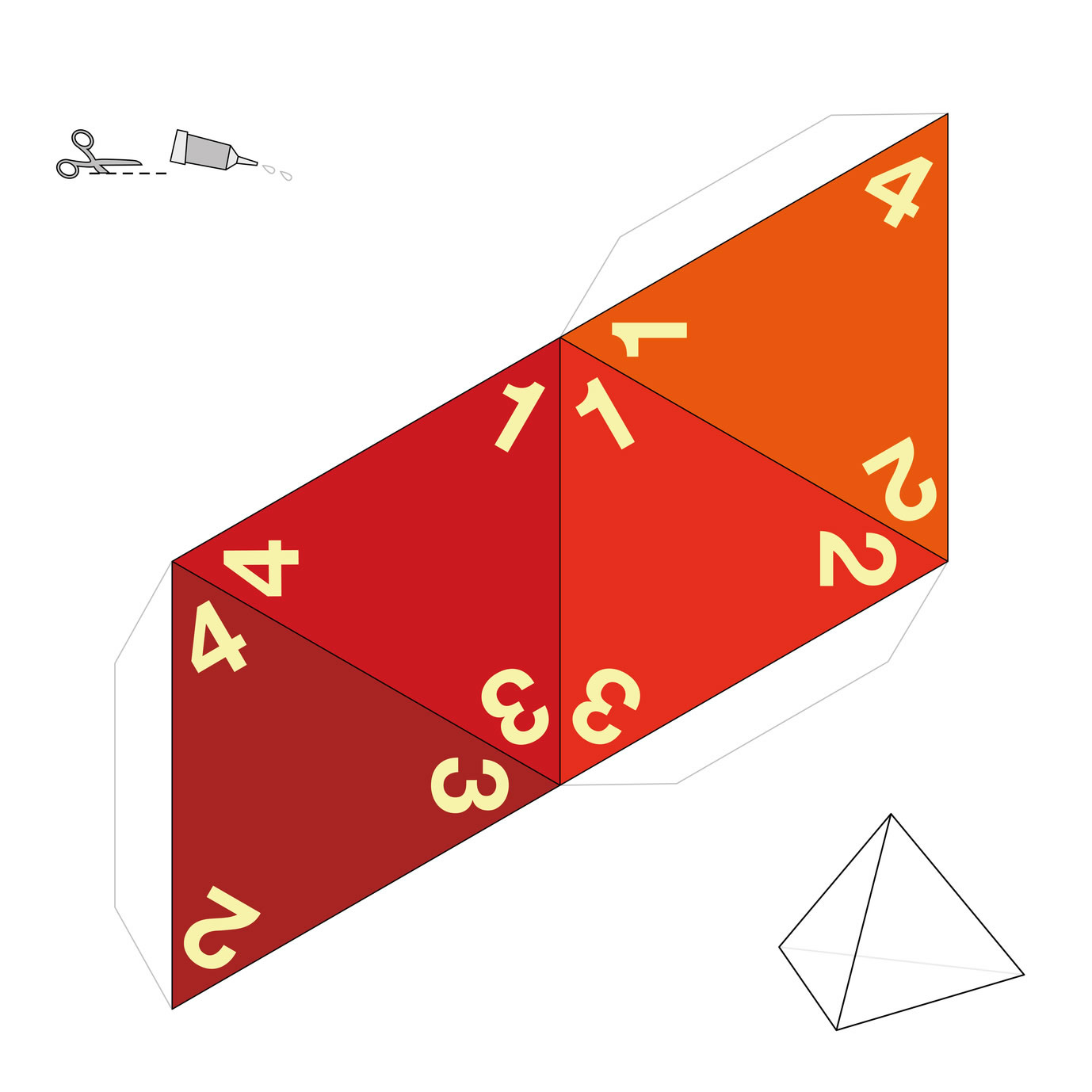
Tämä geometrinen kuvio koostuu neljästä tasasivuisesta kolmiosta eli säännöllisistä kolmioista. Toisin sanoen se on säännöllinen monitahoinen, jossa on neljä yhtä suurta kolmiomaista pintaa. Tällä polyhedronilla on yhteensä neljä pintaa, kuusi reunaa ja neljä kärkeä (kolme pintaa kohtaavat sen jokaisessa kärjessä).
Mitä tulee sen korkeuteen, se saadaan vetämällä kohtisuora kärjestä tämän kuvion vastakkaiseen pintaan. Sen tilavuus on kolmasosa pohjan pinta-alasta kerrottuna sen korkeudella. Pinta-alan laskemiseksi lasketaan yhden kolmion pinta-ala ja kerrotaan neljällä.
On myös epäsäännöllisiä tetraedrejä, jotka koostuvat neljästä eri polyhedrasta. On olemassa kaksi muunnelmaa: kolmikulmainen ja isofacial. Ensimmäisessä on kolme suorakulmaisten kolmioiden muodostamaa pintaa ja niiden korkeudet ovat samassa pisteessä. Toinen koostuu kolmesta tasakylkisessä kolmiossa.
Geometrinen hahmo, jolla on mystinen ja terapeuttinen arvo
Kreikkalainen filosofi Platon ymmärsi, että koko maailmankaikkeus voidaan tiivistää viiteen geometriseen kuvioon: tetraedri, kuutioheksaedri, oktaedri, dodekaedri ja ikosaedri. Ne kaikki tunnetaan yhdellä nimellä, "platonisilla kiinteillä aineilla". Näiden kiinteiden aineiden yhdistelmä muodostaisi pallon, joka edustaisi kosmoksen pyhää geometriaa.
Platonille tetraedri symboloi luonnon elementtiä, tulta (samaan aikaan tämä hahmo liittyy viisauden käsitteeseen). Heksaedri edustaa maata. Oktaedri edustaa ilmaa. Dodekaedri symboloi eetteriä.
Lopuksi ikosaedri edustaa vettä. Joidenkin pseudotieteellisten tulkintojen mukaan nämä luvut liittyvät suoraan joihinkin elävien organismien fysikaalisiin muutoksiin ja näin ollen niiden avulla on mahdollista parantaa joitain sairauksia.
Luonnon kuviot voidaan ilmaista matemaattisella kielellä
Toisaalta jotkut tutkijat väittävät, että maailmankaikkeuden kieli liittyy platonisiin kiinteisiin aineisiin. Tämä tarkoittaa, että fyysinen maailma on järjestetty matemaattisten ominaisuuksien mukaan.
Matemaattiset mallit ovat läsnä tähtikuvioissa, ihmiskehossa, taiteessa ja kaupungeissa, joissa asumme. Geometristen hahmojen avulla voimme jopa ymmärtää aineen subatomisia osia. Platon ja Pythagoraan koulukunnan filosofit esittivät tämän todellisuuden intuitiivisella tavalla.
Tiedemiehet keskustelevat tästä kysymyksestä edelleen tänään. Joillekin luonto on kirjoitettu matemaattisella kielellä ja toisille mielemme luo matemaattisia malleja luonnon ymmärtämiseksi.
Kuva: Fotolia - Peter Hermes Furian
